Глава 4. Искривленное Время и Пространство, и Приливная Гравитация

Искривленное Время и Пространство, и Приливная Гравитация

(И)

Закон Эйнштейна об Искривлении Времени

Эйнштейн бился над постижением гравитации начиная с 1907 года. Наконец, в 1912 году его посетило блестящее озарение. Время, понял он, должно искривляться массой тяжелых тел, таких как Земля или черная дыра, и это искривление в ответе за гравитацию. Он воплотил это озарение в том, что я называю "законом Эйнштейна об искривлении времени", - это точная математическая формула,[8] которую я качественно описываю так: Все хочет жить там, где оно будет стареть медленнее всего, и гравитация влечет его туда.

Чем больше замедление времени, тем сильнее гравитационное тяготение. На Земле, где замедление времени составляет всего несколько микросекунд в день, тяготение скромное. На поверхности нейтронной звезды, где время замедляется на несколько часов в день, тяготение огромно. На поверхности черной дыры время замедляется вплоть до остановки, и там тяготение столь чудовищно, что ничто не может выбраться, даже свет.

Замедление времени около черной дыры играет важную роль в Интерстелларе. Купер отчаивается когда-либо снова увидеть свою дочь Мерф, когда в путешествии вблизи Гаргантюа для него проходит несколько часов, в то время как Мерф на Земле состаривается на восемь десятилетий.

Человеческие технологии оказались слишком хилыми и не позволили проверить закон Эйнштейна в течение почти полувека после того, как он сформулировал его. Первая хорошая проверка состоялась в 1959 году, когда Боб Паунд и Глен Ребка, используя новую технологию под названием эффект Мессбауэра, сравнили скорость течения времени у основания 73-футовой башни Гарвардского Университета со временем на вершине башни. Их эксперимент был превосходно точным - достаточно точным, чтобы заметить разницу в 0,0000000000016 секунды (1,6 триллионной доли секунды) за день. Отметим, что они обнаружили разницу в 130 раз больше этой погрешности, прекрасно согласовывающуюся с законом Эйнштейна: в основании время течет медленнее чем на вершине на 210 триллионных секунды каждый день.

Точность увеличилась в 1976 году, когда Роберт Вессот из Гарварда на ракете НАСА отправил атомные часы на высоту 10 000 километров, используя радиосигналы для сравнения скорости их хода с часами на земле (рисунок 4.1). Вессот обнаружил, что время на земле течет медленнее по сравнению с высотой в 10 000 километров примерно на 30 микросекунд (0,00003 секунды) в день, и его измерения согласовывались с законом Эйнштейна об искажении времени в пределах погрешности измерения. Эта погрешность составляла семь стотысячных: 0,00007 из 30 микросекунд в день.

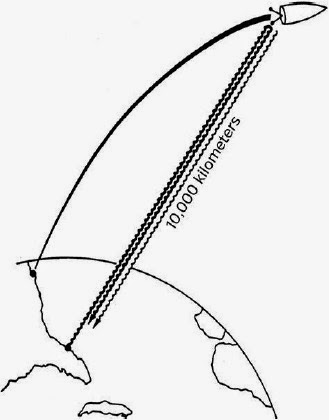
Рис. 4.1. Атомные часы измеряют замедление времени на Земле. [Репродукция из Был ли Эйнштейн Прав? Проверяя Общую Теорию Относительности Клиффорда М. Уилла (Basic Books, 1993).]

Система GPS (англ. the global positioning system), с помощью которой наши смартфоны могут сказать, где мы находимся, с точностью до 10 метров, полагается на радиосигналы комплекса из 27 спутников на высоте 20 000 километров (рисунок 4.2). Обычно от четырех до двенадцати спутников видны одновременно с любой позиции на Земле. Каждый радио сигнал сообщает смартфону, где находится спутник, и время, когда сигнал был отправлен. Смартфон засекает время прибытия сигнала и сравнивает его со временем отправления, чтобы узнать, далеко ли сигналу пришлось пройти - узнать расстояние между спутником и телефоном. Зная положение и расстояние нескольких спутников, смартфон триангуляцией высчитывает собственное положение.

Эта схема провалилась бы, принимай спутники за время отправки сигнала по-настоящему измеренное ими время. Время на высоте 20 000 километров течет быстрее, чем на Земле, на 40 микросекунд в день, и спутники должны учитывать эту поправку. Они измеряют время своими собственными часами, а затем замедляют это время до скорости течения времени на Земле, прежде чем отправить его на смартфон.

Рис. 4.2. Система GPS.

Эйнштейн был гением. Возможно, величайшим ученым всех времен. Это один из многих примеров того, как его озарения касательно законов физики не могли быть проверены в его дни. Потребовалось полвека, чтобы технология развилась достаточно для проведения высокоточного эксперимента, и еще полвека, чтобы описанные им явления стали частью повседневной жизни. Среди других примеров лазер, ядерная энергия и квантовая криптография.

Искривление Пространства: Балк и Наша Брана

В 1912 году Эйнштейн понял, что если время искривляется массивными телами, то и пространство, должно быть, тоже искривляется. Но несмотря на самый мощный мозговой штурм в его жизни, подробности искривления пространства долго от него ускользали. Он бился с 1912 до позднего 1915 года. Наконец, в ноябре 1915 года, в миг великой Эврики он сформулировал свое "уравнение поля общей теории относительности", содержавшее все его релятивистские законы, включая искривление пространства.

И вновь, человеческие технологии оказались хиловаты для высокоточной проверки.[9] На этот раз для необходимых улучшений потребовалось шестьдесят лет, завершившихся несколькими ключевыми экспериментами. Больше всего мне нравится эксперимент, проведенный Робертом Ризенбергом и Ирвином Шапиро из Гарварда. В 1976-77 годах они транслировали радиосигналы двум космическим аппаратам на орбите Марса. Аппараты, Викинг 1 и Викинг 2, усилили сигналы и отправили их назад на Землю, где было измерено время пути сигналов туда и обратно. По мере того, как Земля и Марс двигались вокруг Солнца по своим орбитам, радиосигналы перемещались по изменяющимся траекториям. Сначала траектории проходили далеко от Солнца, потом приблизились, а затем снова удалились, как показано в нижней части рисунка 4.3.

Рис. 4.3. Время пути радиосигналов от Земли до Викинга и снова до Земли.

Если бы пространство было плоским, время пути туда и обратно изменялось бы ровно и постепенно. Но нет. Когда радиоволны проходили близко к Солнцу, их путь занимал больше времени, чем ожидалось, на сотни микросекунд. Добавочное время показано на рисунке 4.3 как функция от положения космического аппарата; оно возрастало, а затем снова убывало. Теперь, один из законов теории относительности гласит, что радиоволны и свет распространяются с абсолютно постоянной, неизменной скоростью.[10] Таким образом, расстояние от земли до космического аппарата должно было быть длиннее ожидаемого, когда волны проходят мимо Солнца, длиннее на сотни микросекунд, помноженные на скорость света: около 50 километров.

Эта увеличенная длина была бы невозможной, если бы пространство было плоским, как лист бумаги. Она появляется из-за искривления пространства возле Солнца. Исходя из того, как менялась задержка сигнала по мере движения аппарата по отношению к Земле, Ризенберг и Шапиро вывели форму пространственного искажения. Точнее, они вывели форму двухмерной поверхности, образованной траекториями радиосигналов от Викингов. Эта плоскость очень близка к экваториальной плоскости Солнца, так что я так и буду тут ее описывать.

Измеренная форма, для экваториальной плоскости Солнца, показана на рисунке 4.4 с преувеличенной амплитудой искривления. Измеренная форма была точно такой, как предсказывала теория относительности - в пределах экспериментальной ошибки, которая составляла 0,001 реальной кривизны, то есть одну тысячную. Возле нейтронной звезды искривление пространства куда больше. Возле черной дыры - чудовищно больше.

Теперь, экваториальная плоскость Солнца делит пространство на две одинаковые половины, над плоскостью и под ней. И все же, на рисунке 4.4 видно, что эваториальная плоскость изогнута как поверхность чаши. Она выгнута вниз внутри и вблизи Солнца, так что диаметры окружностей вокруг Солнца, умноженные на π (3,14159…), получаются больше длин этих окружностей - в случае Солнца, больше примерно на 100 километров. Не так уж много, но это легко измерил космический аппарат с точностью до одной тысячной.

Как может быть пространство "выгнуто вниз"? Куда оно выгнуто? Оно выгнуто в гиперпространство с большим числом измерений, так называемый "балк", которое не является частью нашей Вселенной!

Давайте уточним. На рисунке 4.4 экваториальная плоскость Солнца представляет собой двухмерную плоскость, выгнутую в трехмерный балк. Так же мы, физики, представляем и всю нашу Вселенную. У Вселенной три пространственных измерения (север-юг, запад-восток, верх-низ), и мы представляем себе ее как трехмерную мембрану, или коротко брану, искривленную в более высокоразмерном балке. Сколько у балка измерений? Я детально обсужу это в Главе 21, но для Интерстеллара балку нужно всего одно дополнительное измерение - всего четыре пространственных измерения.

Теперь, человеку очень трудно наглядно вообразить, как наша трехмерная Вселенная, вся наша брана, живет и изгибается в четырехмерном балке. Так что в этой книге, рисуя картинки с браной и балком, я убираю одно измерение, как на рисунке 4.4.

Рис. 4.4. Траектории радиосигналов Викингов в искривленной экваториальной плоскости Солнца.

В Интерстеллар персонажи постоянно ссылаются на пять измерений. Три из них - пространственные измерения нашей Вселенной-браны (север-юг, запад-восток, верх-низ). Четвертое - время, а пятое - дополнительное пространственное измерение балка.

Существует ли вправду балк? Есть ли настоящее пятое измерение, а может и больше, недоступное человеческому опыту? Очень похоже, что да. Мы исследуем это в Главе 21. Искривление пространства (искривление нашей браны) играет большую роль в Интерстелларе. Например, оно является ключом к самому существованию кротовой норы, соединяющей Солнечную систему с отдаленными уголками Вселенной, где обитает Гаргантюа; оно же является гравитационной линзой, которую мы видели на рисунке 3.3.

На рисунке 4.5 изображена крайняя форма пространственной кривизны. Эта фантастическая зарисовка моего друга, художницы Лии Хэллоран, изображает гипотетическую область нашей Вселенной с большим количеством кротовых нор (Глава 14) и черных дыр (Глава 5), которые выступают из нашей браны и проходят через балк. Черные дыры заканчиваются острыми точками, так называемыми "сингулярностями". Кротовые норы соединяют один участок нашей браны с другим. Как обычно, я пропускаю одно из трех измерений нашей браны, так что она выглядит как двухмерная поверхность.

Рис. 4.5. Черные дыры и кротовые норы, выступающие из нашей браны и проходящие в балке. Одно пространственное измерение удалено и у браны, и у балка. [Рисунок художницы Лии Хэллоран.]

Приливная Гравитация

Теория относительности Эйнштейна велит планетам, звездам и космическим кораблям без тяги двигаться возле черной дыры по самой прямой траектории, какую позволяет искривленное время и пространство. На рисунке 4.6 показаны примеры таких траекторий. Две розовые траектории, направленные внутрь черной дыры, начинаются параллельно друг другу. Каждая из них старается остаться прямой, и они сходятся вместе. Искривление пространства и времени сводит их вместе. Зеленые траектории, движущиеся по касательной к черной дыре, тоже начинаются параллельно. Но в этом случае искривление разводит их прочь друг от друга.

Рис. 4.6. Четыре траектории планетарного движения в окрестностях черной дыры. Изображение дыры вырезано из зарисовки Лии Хэллоран, рисунок 4.5.

Несколько лет назад я и мои студенты открыли новый взгляд на эти планетарные траектории. В теории относительности есть математическая величина под название тензор Римана. Он описывает детали искривления пространства и времени. Мы обнаружили скрытые в математических недрах тензора Римана силовые линии, которые сжимают вместе одни планетарные орбиты и растягивают прочь другие. "Тендекс-линии" (англ. tendex lines), как окрестил их мой студент Дэвид Николс, от латинского слова tendere, означающего "растягивать".

На рисунке 4.7 показаны несколько тендекс-линий вокруг черной дыры с рисунка 4.6. Зеленые траектории правыми концами начинаются параллельно друг другу, а затем красные тендекс-линии растягивают их прочь друг от друга. Я нарисовал женщину на красной текдекс-линии. Ее тоже растягивает, она чувствует растягивающую силу между головой и ногами, вызванную красной тендекс-линией.

Рис. 4.7. Тендекс-линии вокруг черной дыры. Изображение дыры вырезано из зарисовки Лии Хэллоран, рисунок 4.5.

Розовые траектории с верних концов идут параллельно друг другу. Потом синие тендекс-линии сжимают их вместе, и женщина, лежащая вдоль синей тендекс-линии, тоже сжимается.

Это растягивание и сжимание - просто еще один способ представить влияние кривизны пространства и времени. С одной точки зрения, траектории сходятся и расходятся из-за того, что движутся по самому прямому маршруту из возможных в искривленном пространстве и времени. С другой, это тендекс-линии растягивают и сжимают. Следовательно, тендекс-линии должны каким-то глубинным образом выражать искривление пространства и времени. И это действительно так, как показала математика тензора Римана.

Черные дыры - не единственное, что создает растягивающие и сжимающие силы. Их создают также звезды, планеты и их спутники. В 1687 году Исаак Ньютон обнаружил их в собственной теории гравитации и использовал это для объяснения океанических приливов.

Гравитация Луны притягивает ближнюю сторону Земли сильнее, чем дальнюю, заключил Ньютон. А притяжение боков Земли направлено чуть внутрь, потому что направление к центру Луны немного отличается для разных боков. Это общепринятая точка зрения на гравитацию Луны, изображенная слева на рисунке 4.8.

Рис. 4.8. Ньютоновское объяснение земных океанических приливов.

А теперь, Земля не ощущает среднего значения этих гравитационных притяжений, потому как свободно падает по своей орбите.[11] (Так же, как и экипаж Эндуранс не ощущает гравитационного тяготения Гаргантюа, пока находится на Эндуранс, на парковочной орбите над черной дырой. Они ощущают только центробежные силы из-за вращения Эндуранс.) Что Земля все-таки ощущает, так это лунные тяготения, отмеченные красными стрелками в левой части рисунка 4.8 с вычтенным средним значением; то есть, она ощущает растягивание в направлении Луны и сжатие с боковых сторон (правая половина рисунка 4.8). Это качественно то же самое, что и рядом с черной дырой (рисунок 4.7).

Эти ощущаемые силы оттягивают океан от земной поверхности на ближней и дальней от Луны сторонах, создавая там прилив. И прижимают океаны к земной поверхности на боковых сторонах Земли, вызывая отлив. По мере того как Земля вращается вокруг своей оси, совершая один полный оборот каждые двадцать четыре часа, мы видим два прилива и два отлива. Так Ньютон объяснял приливные силы, не учитывая маленькую сложность - приливная гравитация Солнца тоже способствует приливам. Его растягивания-сжатия складываются с растягиваниями-сжатиями Луны.

Из-за участия в формировании океанических приливов, эти сжимающие и растягивающие гравитационные силы - силы, которые Земля ощущает, - называют приливными силами. С очень высокой точностью приливные силы, рассчитанные с помощью законов Ньютона, совпадают с теми, что рассчитываются через теорию относительности. Они и должны совпадать, поскольку теория относительности и законы Ньютона всегда дают одинаковые результаты, когда гравитация слаба и тела движутся намного медленнее света.

В релятивистском описании лунных приливов (рисунок 4.9) приливные силы создаются синими тендекс-линиями, сжимающими Землю с боков, и красными тендекс-линиями, растягивающими ее в напровлении Луны. Это очень похоже на тендекс-линии черной дыры (рисунок 4.7). Тендекс-линии Луны - это визуальное воплощение искривления Луной пространства и времени. Удивительно, что такое крошечное искривление создает силы, способные вызвать океанические приливы!

Рис. 4.9. Релятивистский взгляд на приливы: они создаются тендекс-линиями Луны.

На планете Миллера (Глава 17) приливные силы чудовищно больше, и они являются ключом к разгадке гигантских волн, с которыми сталкиваются Купер и его команда.

Теперь у нас есть три взгляда на приливные силы:

• Взгляд Ньютона (рисунок 4.8): Земля не чувствует полное гравитационное тяготение Луны, но чувствует полное тяготение (которое разнится по поверхности Земли) минус усредненное тяготение.
• Тендексный взгляд (рисунок 4.9): Тендекс-линии луны растягивают и сжимают земные океаны; а также (рисунок 4.7) тендекс-линии черной дыры сводят и разводят траектории планет и звезд вблизи черной дыры.
• Взгляд прямого маршрута (рисунок 4.6): траектории звезд и планет вблизи черной дыры - это самые прямые маршруты из возможных в искривленном дырой пространстве и времени.

Три точки зрения на одно явление могут быть крайне ценными. Ученые и инженеры тратят большую часть жизни на решение головоломок. Головоломка может быть в том, чтобы спроектировать космический корабль. Или выяснить, как ведет себя черная дыра. В чем бы не заключалась головоломка, если один взгляд не приносит результатов, может помочь другой. Пока разглядываешь проблему то с одной, то с другой точки зрения, зачастую приходят новые идеи. Вот что делает Профессор Бранд в Интерстелларе, пытаясь понять и обуздать гравитационные аномалии (Главы 24 и 25). И на это я потратил большую часть своей сознательной жизни.

---

8. См. Кое-Какие Технические Заметки в конце книги.

9. Хотя, см. первый раздел Главы 24.

10. Неизменной после хорошо изученной поправки на небольшое замедление из-за взаимодействия с электронами в межпланетном пространстве - так называемая "поправка на плазму" (англ. plasma corrections).

11. В 1907 году Эйнштейн осознал, что если бы ему довелось свалиться, скажем, с крыши своего дома, то во время падения он не чувствовал бы гравитации. Он назвал это "самой радостной мыслью в жизни", потому что с нее начались его поиски понимания гравитации, поиски, которые привели к его концепции искривленного времени и пространства и к законам, управляющим этим искривлением.

- Предыдущая Глава - Содержание - Следующая Глава -